A guided tour to the MECS
and to its response matrix
This set of HTML pages has been written by
Lucio Chiappetti (
IFCTR)
with substantial input from the entire
MECS team,
and in particular by
Teresa Mineo
and Cettina Maccarone
(IFCAI).
Navigation through the tour is possible in an ordered way
using the Table of Content, or
the activated navigation "buttons" at the end of each page, or randomly
just following the links or clicking on images.
We give here a quick description of the Medium Energy Concentrator Spectrometer (MECS)
[1]
on board
the BeppoSAX satellite.
In particular we give some information on the content of the various
calibration files,
their meaning and role (with particular, but not exclusive, regard to those
entering the generation of the response matrix).
All values (even those inlined in the text, or plotted) will be produced on-line from
the latest calibration files, in order to guarantee an automatic update.
Note that, for plots produced by IDL, we cannot guarantee availability of a free license
at all times. If a plot cannot be produced, please try later.
The MECS consists of three units (hereafter named M1, M2, and M3),
each composed of a grazing incidence Mirror Unit (MU), and of a
position sensitive Proportional Counter (GSPC) located at the focal plane.
The MUs are connected to the GSPCs by a carbon fiber envelope, ~2 m long.
The following interactive map gives an impression of the components of one MECS unit.
You may click on the various items and labels to access information about
the MECS components or
the MECS calibration parameters.
Note that the vertical scale is magnified by about a factor 8
and some items have been
exploded from their actual position for clarity. The carbon fiber optical
envelope connecting mirrors and detector is not shown.
![[MECS interactive map]](mecs.gif)
Fig. 1.1-I : MECS interactive map
The response matrix of an X-ray detector allows to reconstruct source photon
spectra from the observed counts (counts per Pulse Height Analyser [PHA] or Pulse Invariant
[PI] channels).
The detected count spectrum is in fact given by the convolution
of the actual photon spectrum by the response matrix:
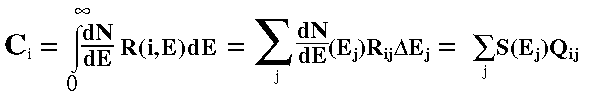 (1)
(1)
[Click on each formula element to see its dimensions (physical units)]
where Ci are the detected counts in the
i-th
PI channel dN/dE is the photon input spectrum, R is the overall response
matrix and j runs on a discrete binning of the photon input energy E,
each j-th bin with
DeltaEj width.
In formula (1) the matrix Qij corresponds to the
XAS-format matrix file and has dimensions of [cm2 keV] however
it is customary to use Rij as overall response matrix and to decompose it in two terms :
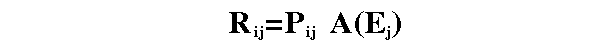 (2)
(2)
where:
- Pij is the redistribution matrix
(the adimensional probability that a photon
of input energy Ej is detected
in channel i) which correspond to an OGIP RMF file
- the 1-d array A(Ej)
is the total effective area has dimensions of an area
[cm2] and includes all
contributions which depend only on the input photon energy and corresponds
to an OGIP ARF file. For the MECS this is the overall
effective area.
- (in the case of the MECS there are no terms which depend on the PHA/PI channel only)
The following (conventional or real) components enter in the computation of the response
matrix :
The overall redistribution matrix can therefore be obtained as a sum of several terms
(click on each formula component for details) as indicated below.
Index k runs on the four main Xenon escape peaks.
Note that not all terms are defined in all energy ranges.
Also probabilities G and T are appropriately normalized for
escape fractions
in such a way that the total probability of a photon of energy Ej to spread over all
channels is unity (except close to the extrema of the energy range where a photon
may be lost out of the useful range).
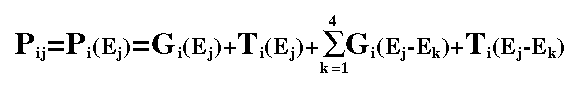 (3)
(3)
A flow-chart of the calculation if the RMF in the
XAS MECS matrix accumulation program
is given in Fig. 1.2.1-I
The effective area as a function of energy is the product of several array or
scalar terms. Some of these terms also depend on other parameters, like the position on
the detector ,or the burst length limits.
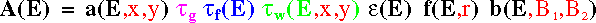 (4)
(4)
The terms entering the above formula (click on each factor to access relevant information) are
:
A flow-chart of the calculation if the RMF in the
XAS MECS matrix accumulation program
is given in Fig. 1.2.2-I
The position and energy of a photon are computed by the
Electronics Unit
based on the output of the
PMT.
This process introduces distortions both in position and gain because of
three effects :
- spatial disuniformity of the PMT gain (energy independent)
- different viewing angles of different scintillation positions (energy independent)
- curvature of the
Be window
with associated distortion of the electric field (energy dependent)
The relevant distortions have been modelled using ground measurements based on a
multipinhole mask
; the modeling is given as a
relation
converting unlinearized x,y pixel positions into
linearized X,Y
positions in mm, and as a
map
to correct for the position dependency of the gain.
Moreover, variations in the detector temperature produce sligthly changes in
the gain that are corrected with respect to an
absolute reference.
There are a number of calibration parameters
that are typically used in
corrections performed during data accumulation.
We give here a quick reference list, with pointers to
details kept elsewhere :
The final effect of the gain corrections is to convert PHA channels
into PI channels.
There are a number of calibration parameters which do not enter
in the computation of the response matrix or in the corrections
performed during data accumulation, but useful for the attitude reconstruction
and data analysis. We give here a quick reference list,
with pointers to details kept elsewhere :
An invited paper
[3]
discussing the current knowledge of the analysis about the instrumental and cosmic background observed by the MECS has been presented at the RXTE/BeppoSAX Lincei conference
"The Active X-ray sky" in Rome, 21-24 Oct 1997
(see preprint in
astro-ph/9712251
or locally a
preview)
The reader is referred to such paper for details. There are at present no standard XAS calibration files related to the background, although some material has been released
by SDC. We recall here only the most important issues.
The background observed by the MECS is constituted by several components :
- the instrumental background, in turn comprising
- the cosmic background, whose description is beyond the present scope, but which
is affected by the following calibration effects :
For the above reasons, it may not be wise to use as background subtraction the naive method
of extracting gross source counts from a small circular region, and subtracting the
background from a surrounding annulus. In fact the spectrum of the annulus is likely to
be affected by the following effects :
- a non negligible fraction of the PSF of the source
(a few percent) may be contaminating it
- the cosmic contribution will be underestimated because of vignetting effects
- the residual calibration events may be higher than in the
detector centre
For these reasons it is advisable to subtract a blank field background accumulated in
the same region where the source is extracted.
[Home]
[ToC]
[Previous]
[Next]
sax.iasf-milano.inaf.it/Sax/Mecs/
:: original creation 2007 Sep 13 12:05:00 CEST ::
last edit 2007 Sep 13 12:05:00 CEST
![[MECS interactive map]](mecs.gif)
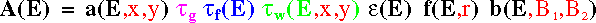 (4)
(4)